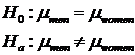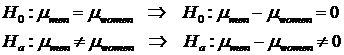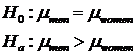Type I and Type II Errors
Lecture 5

Hypothesis Tests

1. We take one sample and we calculate the mean

   1. The Mean is the estimator of the true population parameter

   2. Build a confidence interval, using a specific a, such as a = 0.05

   3. There is a 95% chance that the true population mean lies within an interval

2. We take a second sample, and we get a different mean and confidence interval

   • We can test if these two sample means come from the same population or from different ones

3. Example – Average income for men and women

   1. Men earn on average $40,000 per year

   2. Women earn on average $30,000 per year

4. Hypothesis Test

   1. We test whether the population parameters are the same or different

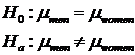
2. m _men: Population mean for men’s income

3. mm _women: Population mean for women’s income

4. Also, these hypothesis test are equivalent

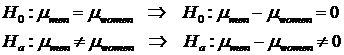
5. A hypothesis test has to cover all situations

   1. This hypothesis test is invalid

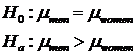
2. We are missing the case whether women have higher incomes than “ men

6. We choose a Significance Level, a

   1. Type I Error – the error we make when we reject the true hypothesis, H ₀

      1. This occurs a% of the time

   2. Type II Error – the error we make when we fail to reject a false null hypothesis

      1. Denoted by b probability

      2. We cannot observe this in the data

   3. Usually researchers set a = 0.1, 0.05, or 0.01

      1. These a’s have a good balance between Type I and Type II errors

   4. Example

      1. Choose a = 1 x 10 ^-6

      2. The Type I error becomes smaller, but the Type II error becomes larger

      3. You are increasing the chances of “failing to reject” a false null hypothesis

7. The Power is defined as 1 – b

   1. The Power is the probability we reject the null hypothesis when it is false

   2. We want 1 – b to be high

   3. How do we increase the power?

      1. The larger the number of observations, the more information we have; the more power

      2. The type of statistical test

An example of a Hypothesis Test

1. Testing the Hypothesis if two sample means come from the same population

   1. Example

      1. Assuming s is known, thus we use the normal distribution

      2. We know from the table

   	Average Income	Observations	Standard Deviation
   Men	$40,000	200	$10,000
   Women	$30,000	150	$5,000

   3. We must combine the variances

   4. We are assuming the variances are the same

   2. Calculate the Standard Error (SE)

   

   3. The z-test

   

   4. In Excel, we can calculate the p-value for this z statistic

      1. The function, =normdist(value, mean, std. deviation, cumulative)

      2. value is the z statistic

      3. mean is zero, because it has been standardized

      4. std. deviation is 1, because it has been standardized

      5. cumulative =1. We are calculating areas under the PDF (which is actually the CDF)

      6. The p-value = 1.55 x 10 ^-34

   

   5. Two cases

      1. If the z is positive, then Excel returns [-z, z], so subtract the p-value from 1 to get the positive tail

      2. If the z is negative, then Excel returns the proper p-value for a left side tail

   6. We usually do a two tail test

      1. We divide a by 2 and put this probability in each tail

      2. The two tail test is shown below

2. Three ways to test a hypothesis

   1. z-statistic

      1. Reject the null hypothesis, if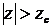

      2. In our case, our z-value is 12.2 and our critical z is 1.96

      3. Thus, reject the H ₀ and conclude men and women have different income levels

   2. p-values

      1. Reject the null hypothesis, if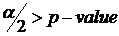

      2. In our case, our p-value is 1.55 x 10 ^-34 while our critical probability is 0.025

      3. Thus, reject the H ₀ and conclude men and women have different income levels

   3. Confidence intervals

      1. We can construct confidence intervals the test hypothesis

      2. This method is shown in the next lecture

3. In reality, we never know the population parameter, s ²

   1. Thus, when we estimate s ², then we switch the distribution to a t-distribution

   2. The analysis is the same; however, the methods to pool variances look more complicated

4. We only examined two-tail hypothesis test; however, this analysis can be applied to one tail hypothesis tests