Differences between Percentages and Paired Alternatives
Lecture 6

Percentages
 

  1. Apply the same methodology to percentages

Equation 1

    1. Where P is  the percentage calculated from the data while r is the Greek letter that represents the population parameter

    2. Using the same logic, the standard error (SE) is:

Equation 2

    1. The variances are

Equation 3

    1. This test is approximate because we are calculating the variances from the data

    2. Then calculate the z-statistic

  1. Example:

    1. 300 students are randomly chosen (n 1) at Suleyman Demirol

      1. P 1 = 55% are women

      2. 1 – P 1 = 45% are men

    2. 400 students are randomly chosen (n 2) from the business school

      1. P 2 = 60% are women

      2. 1 – P 2 = 40% are men

    3. Are the same percentage of women studying business is the same percentage as the student body?

    4. The hypothesis is:

Equation 1

    1. The standard error (SE) is:

Equation 4

    1. The z-statistic

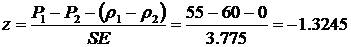
Equation 5

    1. The critical z-value is 1.96. The p-value is 0.092669

      1. Excel, the p-value is calculated from =normdist(-1.3245, 0, 1, 1)

      2. According to both the z and p values, fail to reject the null hypothesis and conclude both percentages are the same

      3. Both the methods will give the same results. The z and p values are testing the same hypothesis from different angles

      4. Note – Excel doubles the p-value for two-tail test

        • Thus, do not use a/2 but only a

  1. You can also use confidence intervals for hypothesis testing

Equation 6

    • The interval contains zero. Thus, fail to reject the null hypothesis.

 

Poisson Distribution
 

  1. The probability of a number of events that occur in a specific time period

    • Counting distribution

      1. Number of events

      2. Number of deaths

      3. Number of births

      4. Number of accidents at a street intersection

  2. The PDF is

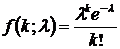
Equation 7

    1. k is the number of occurrences, k = 1, 2, 3, …

    2. l is expected number of occurrences in interval

  1. This distribution is unique, the mean = variance = l

    • Note – Occurrences have to be independent

      1. Example: Epidemic sweeps through in area, increasing the death rate

      2. Event is not independent

  2. Example: Heart disease

    1. In 2008, there were 543 deaths (n 1)

    2. In 2009, there were 674 deaths (n 2)

    3. Is this increase in deaths due to chance?

    4. The hypothesis is:

Equation 8

    1. The standard error (SE) is

Equation 9

    1. The z-statistic is:

Equation 10

    1. Using a = 0.05, the z c = 1.96

      1. Reject the null hypothesis and conclude the heart attack rate is higher

      2. The z-statistic is approximate, because it came from a Poisson distribution

 

McNeman’s Test
 

  1. You will not be tested over this test

    1. It is an interesting test

    2. You have an example where your sample has two treatments and the results are paired

    3. Your sample had two experimental medications

    4. A matrix of your results


 Treatment A Treatment B
Outcome 1 Responded Responded
Outcome 2 Responded Did not respond
Outcome 3 Did not respond Responded
Outcome 4 Did not respond Did not respond

  1. You are interested if Treatment A is better than Treatment B?

    1. Ignore Outcomes 1 and 4

    2. Focus on Outcomes 2 and 3

    3. Observations have to be paired

    4. Example:

      1. Each person gets both treatments

      2. Or the sample is divided by 2 and then randomly pair one person to another

  2. Example: 200 people with heart problems

    1. Treatment A: Patients have to eat right and exercise

    2. Treatment B: Patients take a drug, Plavix

    3. Randomly pair sample into 100 pairs


 Treatment A Treatment B Observations
Outcome 1 Responded Responded 15
Outcome 2 Responded Did not respond 30
Outcome 3 Did not respond Responded 45
Outcome 4 Did not respond Did not respond 10



100

    1. The n 1 = 45 and n 2 = 30

    2. Calculate the z-statistic

Equaiton 11

    1. Fail to reject the treatments are the same, because a = 0.05 and the z c = 1.96

    2. Note – I could give all patients both treatments, but I have to discern which treatment did what