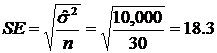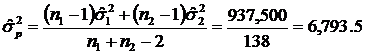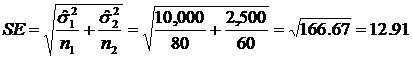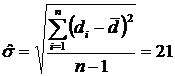The t Tests
Lecture 7

The t Distribution

 

  1. The t-tests are similar to the z-tests

    1. However, you assumed you knew the population variance

    2. In reality, the variance has to be estimated too!

    3. Switch to the t distribution

The t versus the normal distribution

    1. The t-distribution is shorter and fatter because you estimated two parameters, the mean and the variance

    2. The Rule of Thumb

      1. If the observations are less than 30, then use the t-distribution

      2. If the number of observations are equal to or greater than 31, then use the z-distribution as an approximation

  1. Example

    1. You survey 30 people in Almaty. The average income, 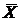Equation 1 = $600 per month and variance, Equation 2 = 10,000

    2. Find the 95% Confidence Interval

      1. Use an a = 0.05 and df = 30 – 1 = 29

      2. Using Excel, = tinv( a, df)

      3. t c = 2.04523

      4. If this was a normal distribution, then z c = 1.96

      5. The standard error (SE) is

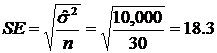
Equation 3

      1. The 95% Confidence Interval is

Equation 4

      1. There is a 95% chance that the true population mean lies between [562.5, 637.5]

Testing the Means between Two Samples

 

  1. Testing the Difference of the means of two samples

    1. This is more complicated because you are estimating the variance

    2. Two methods

      1. If the variances are equal, then pool the variances

      2. If the variances are unequal, then use a different method to pool the variance

    3. Assume the variances are equal

    4. Example

      1. You survey 80 people at Mega Center

        1. The average income is Equation 5= $800 per month

        2. The estimated variance is Equation 6= 10,000

      2. You survey 60 people at Thieves’ Market

        1. The average income is Equation 7= $500 per month

        2. The estimated variance is Equation 8= 2,500

      3. Note – you should test data to determine if data is normally distributed

      4. Variance is calculated at

Equation 9

Variance in Sample 1



(n 1 – 1) Equation 6

(80 -1)(10,000)

790,000

Variance in Sample 2



(n 2 – 1) Equation 8

(60 – 1)(2,500) 147,500

Total Variance 937,500

      1. Total degrees of freedom = n 1 – 1 + n 2 – 1 = 80 + 60 – 2 = 138

      2. The pooled variance is

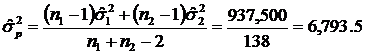
Equation 10

      1. The standard error is

Equation 11

      1. The t-statistic is

Equation 12

      1. If a = 0.05, then the t c = 1.977304

      2. The p-value is 5.01 X 10 -15

      3. The hypothesis test is

Equation 13

      1. Reject the H 0 and conclude the population means are different

    1. Can use a Confidence Interval for hypothesis test

      • If a = 0.05, df = 138, and t c=1.977304

Equation 14

  1. Assume variances are unequal

    1. Same example

    2. The Equation 6=10,000, n 1 = 80, Equation 8=2,500, and n 2 = 60

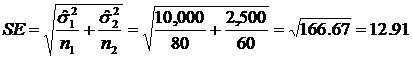
Equation 15

    1. However, we have to adjust the degrees of freedom

Equation 16

    1. Round the degrees of freedom to 122

    2. The t-statistic is

Equation 17

    1. Reject the H 0 and conclude the population means are different

Difference of Means of Paired Observations

 

  1. We have observations that are paired

  2. Two treatments, A and B

  3. Example: Patients are given two types of blood pressure medicine

Observations Treatment A Treatment B Difference
1 64 84 -20
2 67 51 16
3 49 61 -12
. . . .
23 72 70 2

  1. Calculate the average for the differences, Equation 18

  2. Calculate the standard deviation of the differences

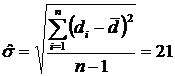
Equation 19

  1. The standard error is

Equation 20

  1. The hypothesis test is

Equation 21

  1. The t-statistic is

Equation 22

  1. The a = 0.05, df = 23 – 1 = 22, and t c = tdist( a, df) = 2.034

    1. Fail to reject the H 0 and conclude both treatments are similar

    2. The paired test is a more powerful test than the other two

    3. Contains more information, because you took the extra step of pairing the observations