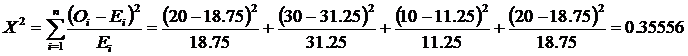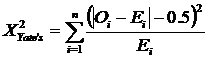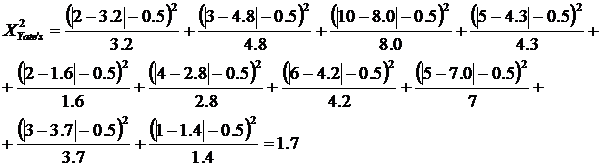The Chi-Square Tests
Lecture 8

Contingency Tables

 

  1. If you take a variable with a normal distribution and square it, then you get a chi-square distribution

  2. Pearson Chi-Square Test

    1. Example: You survey 80 students from a university

      1. Event A: 30 students are men

      2. Event B: 50 students are women

    2. Mutually exclusive – all events have to add up to the total

      • In our case, a male cannot be a woman at the same time, or vice versa

    3. We can test the hypothesis that men and women occur 50/50 in a group

      1. Expected value for men is 40

      2. Expected value for women is 40

    4. Compute the X 2 statistic

Equation 1

    1. Notation

      1. O i is the observed data

      2. E i is the expected

      3. n is the outcomes of each event

Equation 2

    1. The degrees of freedom are df = n – 1 = 2 – 1 = 1

    2. Chi-square test statistic is Equation 3

      1. Reject the H 0

      2. Test statistic is calculated in Excel using =chiinv( a, df)

    3. Note – Chi-squares are one-tail tests, because negative numbers are converted to positive when they are squared

  1. Contingency tables

    1. The simplest is called a 2 X 2

    2. Example: Students took an exam

Occurrences Failed Passed Marginal Total
Male 20 30 50
Female 10 20 30
Marginal Total 30 50 80

    1. You have to use the number of occurrences

      • Do not use percents, proportions, etc.

    2. Have to calculate the expected occurrences from the marginals

Expected Failed Passed Marginal Total
Male Equation 4 Equation 5 50
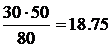
Female Equation 6 Equation 7 30
Marginal Total 30 50 80

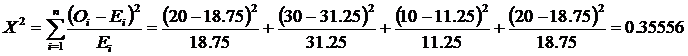
Equation 8 

    1. The degrees of freedom are df = (columns – 1)(rows – 1) = 1 (1) = 1

      1. Chi-square test statistic is Equation 3

      2. Fail to reject the H 0 hypothesis and conclude males and females are equal when taking the exam

    2. Note – There is a fast way to calculate X 2 for a 2 X 2 Contingency Table

Occurrences Failed Passed Marginal Total
Male a b a + b
Female c d c + d
Marginal Total a + c b + d a + b + c +d

Equation 9

    1. Re-doing the example using the fast method

Equation 10

    1. Note – You can build contingency tables with any dimensions

    2. The Chi-square test may be poor if

      1. Grand total is less than 100

      2. Or a cell total is less than 10

      3. Then you should use Yate’s Correction

Yate's Correction
 

  1. Yate’s Correction

Equation 11

    1. Lowers the Chi-square making the statistic more conservative

    2. A simpler formula for the 2 X 2 Contingency Table

Equation 12

    1. Applying the Yate’s Correction to the example

Equation 13

    1. Fail to reject

  1. Expanding the contingency table

    1. An example where the instructor teaches a Forecasting Class

    2. Are the classes different?

Grades Class 1 Class 2 Marginal total
A 2 4 6
B 3 6 9
C 10 5 15
D 5 3 8
F 2 1 3
Marginal total 22 19 41

 

Expected Class 1 Class 2 Marginal total
A 3.2 2.8 6
B 4.8 4.2 9
C 8.0 7.0 15
D 4.3 3.7 8
F 1.6 1.4 3
Marginal total 22 19 41

    1. Perfect for an Excel spreadsheet

Equation 14

    1. The degrees of freedom, df = (5 – 1)(2 – 1) = 4

      1. Chi-square test statistic is Equation 15

      2. Fail to reject the H 0 and conclude the classes are the same

      3. Without the Yate’s Correction, then X 2 = 3.97

    2. Note – the grades have a ranking. This ranking is not included in the statistical test. However, there are other tests that can incorporate the ranking of the grades into the Chi-Square statistic