Exact Probability Test
Lecture 9
Fisher Exact Test
You have to use it if
Values in a cell are below 10
Or the grand total is below 100
Use the Fisher Exact Test
-
Note - Always arrange the columns and rows so Cell A has the smallest number
| Men | Women | Marginal Total | |
| Dieting | a | b | a + b |
| Not Dieting | c | d | c + d |
| Marginal Total | a + c | b + d | a + b + c +d |
Example
| Men | Women | Marginal Total | |
| Dieting | 2 | 10 | 12 |
| Not Dieting | 3 | 5 | 8 |
| Marginal Total | 5 | 15 | 20 |
How many combinations can we make?
Men are the smallest in the study, so we have 5 combinations
Look at the marginal!
The Fisher test uses a Hypergeometric Distribution
Probability of a particular combination, i, is:
Note: 0! = 1
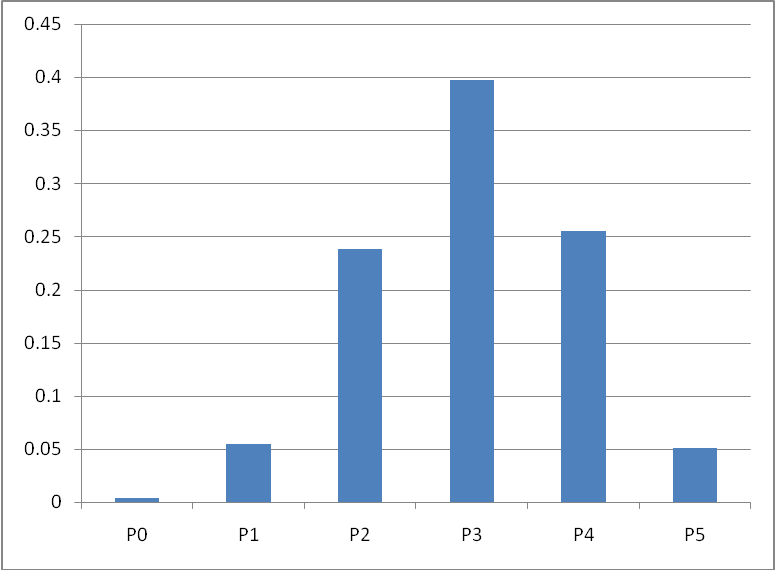
Combination 0
| Men | Women | Marginal Total | |
| Dieting | 0 | 12 | 12 |
| Not Dieting | 5 | 3 | 8 |
| Marginal Total | 5 | 15 | 20 |
Probability of this combination occurring is
Combination 1
| Men | Women | Marginal Total | |
| Dieting | 1 | 11 | 12 |
| Not Dieting | 4 | 4 | 8 |
| Marginal Total | 5 | 15 | 20 |
Probability of this combination occurring is
Combination 2
| Men | Women | Marginal Total | |
| Dieting | 2 | 10 | 12 |
| Not Dieting | 3 | 5 | 8 |
| Marginal Total | 5 | 15 | 20 |
Probability of this combination occurring is
Combination 3
| Men | Women | Marginal Total | |
| Dieting | 3 | 9 | 12 |
| Not Dieting | 2 | 6 | 8 |
| Marginal Total | 5 | 15 | 20 |
Probability of this combination occurring is
Combination 4
| Men | Women | Marginal Total | |
| Dieting | 4 | 8 | 12 |
| Not Dieting | 1 | 7 | 8 |
| Marginal Total | 5 | 15 | 20 |
Probability of this combination occurring is
Combination 5
| Men | Women | Marginal Total | |
| Dieting | 5 | 7 | 12 |
| Not Dieting | 0 | 8 | 8 |
| Marginal Total | 5 | 15 | 20 |
Probability of this combination occurring is
We manually map out the whole probability space for men on a diet
| P0 | 0.0036 | Include in a |
| P1 | 0.0542 | Include in a |
| P2 | 0.2384 | |
| P3 | 0.3973 | |
| P4 | 0.2554 | |
| P5 | 0.0511 | Include in a |
| Total | 1.0000 | a = 0.1089 |
Is our particular combination significant? Are men different than women on a diet?
Our data is P2. If we choose an alpha of 5%, the best we can do in our case is to have an alpha of 11%. We take the probability that is in the tails. Alpha is the sum of P0, P1, and P5. Since our value is P2, we fail to reject and conclude men do not differ from women on a diet.
